Anwendungsgebiete
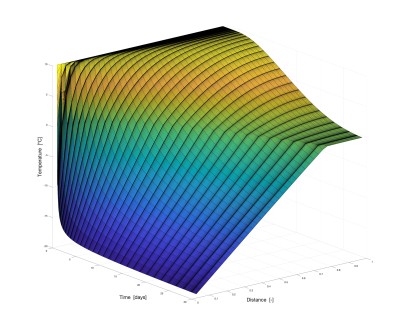
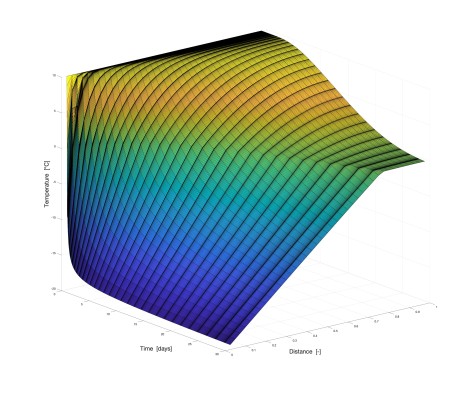
Simulationen werden an unserem Institut in unterschiedlichsten Bereichen erstellt. Ob der Hydratationsprozess von Zement, der Wärmefluss durch unterschiedlichste Materialien, Transportmechanismen oder die Interaktion von Beton mit anderen Materialien untersucht werden sollen, jede Fragestellung kann nicht nur in unseren Laboren praktisch nachgewiesen sondern auch von Simulationen gestützt werden.
Diese Fragestellungen können individuell für sich oder in Kombination betrachtet werden.
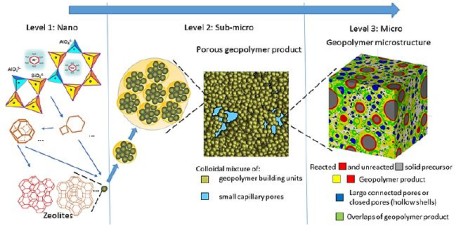
Mit den Simulationen können wir unterschiedliche Einflüsse und Skalenbereiche verbinden. Hierfür kann ein Multiskalenmodell beispielsweise den Einfluss der Mikrostruktur auf meso- bzw. makroskopische Materialeigenschaften liefern.
Programme
Um dieses breite Spektrum abdecken zu können, sind auch sich den Herausforderungen anpassungsfähige Programme bzw. Entwicklungsumgebungen notwendig. Daher arbeiten wir mit auf die Fragestellungen zugeschnittenen Softwarelösungen.
Es können beispielsweise kommerzielle Softwareangebote wie Abaqus für direkte Nachweise und Überprüfungen herangezogen werden. Quelloffene Software kann andererseits bei der Forschung größere Freiheiten und Möglichkeiten zur kreativen Bearbeitung ungewöhnlicher Fragestellungen bieten.
Aber auch Umgebungen wie Matlab oder Python helfen bei Auswertung und Forschung.
Zum Betrachten von mehreren variablen Einflüssen oder der Anwendung der Phasenfeldmethode werden auch Multiphysics-Lösungen wie MOOSE Framework oder openFoam verwendet.
Erfahrungen mit verschiedenen Anwendungen:
Einige Anwendungen, die bereits in zum Teil unterschiedlichen Bereichen zum Einsatz gekommen sind, sind u.a.:
- Abaqus
- Hymostruc
- MOOSE Framework
- OpenFOAM
- PHREEQC
- LAMMPS Molecular Dynamics Simulator
- Matlab
Diese Liste wird kontinuierlich erweitert, um so die besten Lösungen für unsere Forschung und für Untersuchungen zu erzielen.
Rechnerische Ressourcen
Je nach Fragestellung sind unterschiedliche Rechenleistungen notwendig.
Während bei statisch-linearen Berechnungen die Rechenleistung von auf dem Markt standardmäßig verfügbaren Computern ausreichend sein kann, können erhöhte Auflösungen oder Nichtlinearitäten diese Ressourcen bereits überschreiten.
Um hierauf vorbereitet zu sein, stehen Kapazitäten auf unterschiedlichen Stufen zur Verfügung:
Rechner am WiB
Neben den normalen Arbeitsplatzrechner stehen zusätzlich auch für numerische simulationen optimierte Rechner zur Verfügung.
Hierbei handelt es sich um Rechner mit:
- 8-Kern Prozessoren
- bis zu 128GB RAM für nichtlineare Berechnungen mit einer hohen Anzahl an Freiheitsgraden
- NVIDIA Grafikkarten für GPU-Acceleration mittels Cuda
Hichleistungsrechner am WiB
Unser Institut besitzt einen eigenen Hochleistungsrechner (HPC). Das System ist mit der Leistung eines Supermicro GPU-Knotens mit zwei Sockeln, AMD EPYC™ Milan CPUs und 512 GB Speicher ausgestattet. Diese hochmoderne Technologie wird es uns ermöglichen, komplexe Berechnungen mit hoher Geschwindigkeit und Genauigkeit durchzuführen.
Die AMD EPYC™ Prozessoren mit einer hohen Kernanzahl wurden speziell für HPC-Arbeitslasten entwickelt und bieten eine hervorragende Leistung, Skalierbarkeit und Energieeffizienz.
Zusätzliche Grafikkarten (GPUs) beschleunigen rechenintensive Aufgaben wie maschinelles Lernen, Deep Learning und wissenschaftliche Simulationen. Die Kombination dieser leistungsstarken CPUs und GPUs ermöglicht eine schnellere Datenverarbeitung, was zu einer kürzeren Time-to-Intelligence und einer besseren Entscheidungsfindung führt.
Darüber hinaus sind beide Knoten mit insgesamt 768 GB DDR4-RAM ausgestattet, was eine effiziente Verarbeitung großer Datenmengen sowie die Berechnung großer Systeme mit einer hohen Anzahl von Knoten ermöglicht. Dies stellt auch sicher, dass selbst die anspruchsvollsten Anwendungen reibungslos laufen, ohne dass es zu Engpässen oder Verzögerungen kommt.
Mit dieser fortschrittlichen Hardwarekonfiguration ist unser HPC-System in der Lage, eine Vielzahl von Berechnungen durchzuführen, was es unserem Team ermöglicht, einige der anspruchsvollsten Probleme bewältigen zu können.
Diese Fähigkeiten erlauben uns die Simulation von
- komplexer Systeme wie heterogener Materialien mit Millionen von Knotenpunkten
- nichtlineares Materialverhalten, wo hohe Präzision erforderlich ist
- Multiphysik-Simulationen, die die komplexe Kopplung einer eigenen Reihe von PDEs (partiellen Differentialgleichungen) beinhalten und die parallelen Verarbeitungsmöglichkeiten der CPU- und GPU-Architekturen nutzen
- die Analyse riesiger Datenmengen oder die Entwicklung modernster KI-Modelle
- usw.
Dies führt zu detaillierteren und realistischeren Simulationen von komplexen Systemen.
Hochleistungrechner
Sollte die Rechenleistung nicht ausreichen haben wir bereits Erfahrungen am Lichtenberg-Hochleitungsrechner. Hier können zum Beispiel mittels Message Passing Interface (MPI) parallele Berechnungen mit einer großen Menge an Prozessoren parallel genutzt werden, sodass auch sehr komplexe Problemstellungen gelöst werden können.
Hierdurch ist die Rechenleistung am WiB kein limitierender Faktor.
Lichtenberg-Hochleistungsrechner an der TU Darmstadt
Der Lichtenberg-Hochleistungsrechner im Verbund des Hessischen Komptenzzentrum für Hochleistungsrechnen stellt den Nutzern große Rechenkapazitäten von bis zu 3,148 PFlop/s und 257 TByte RAM zur Verfügung.
Weitere Infos sind hier zu finden:
Vorstellung einiger Forschungsbereiche
Am WiB durchgeführte Simulationen
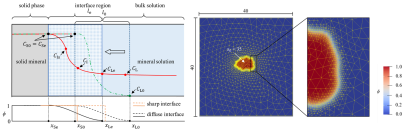
Hier sehen Sie einige Beispiele von vergangenen und aktuellen Simulationen an unserem Institut: